Stift-Malerei mit dem Malstift
|
|
|
|
|
|
|
|
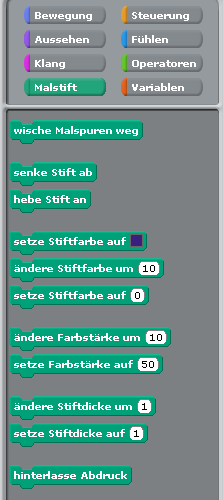Wenn man Figuren bewegt, dann können diese bei der Bewegung Linien auf die Bühne malen. Dazu sind die ‚Malstift‘-Blöcke vorhanden.
Die folgenden Aufgaben sind als Erweiterung zum scratch-Kurs vorgesehen und sollen das Gelernte vertiefen.
Speichert die verschiedenen Programme auf der SD-Karte.
Aufgabe 1, Ein einfaches Quadrat.
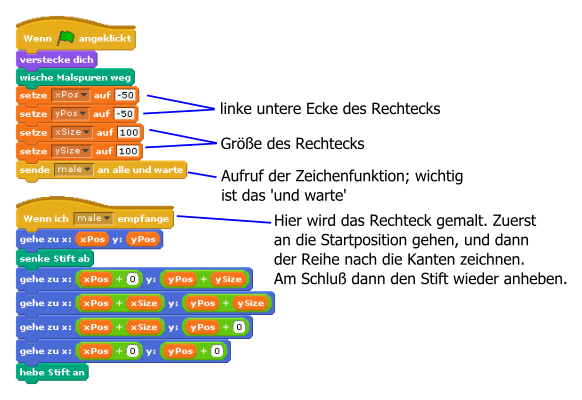
Male mit dem Stift ein Quadrat auf die Bühne, Seitenlänge 100, Position -50,-50 (die linke untere Ecke).
Es gibt mehrere Möglichkeiten für die Lösung.
Programmstruktur
Da solche Quadrate jetzt in vielen verschiedenen Kombinationen verwendet werden lohnt es sich etwas Arbeit in die Programmstruktur zu stecken.
Wenn man Quadrate oder Rechtecke in verschiedenen Größen und Positionen malen will, dann sollte man die Größe und Position in Variablen speichern und dann mit der ‚Sende und Warte‘-Funktion ein anderes Skript aufrufen, was dann die eigentliche Zeichenaufgabe übernimmt.
Das Programm in scratch abtippen und laufen lassen.
Der ‚Sende und Warte‘ -Block kann nicht nur für Quadrate angewendet werden, sondern immer dann wenn man wiederholende Aufgaben ausführen will.
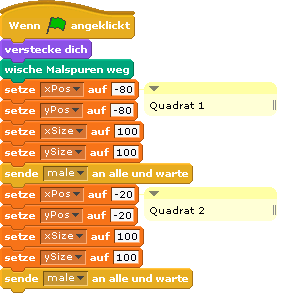
Aufgabe 2: Zwei (?) Quadrate
 |
Man kann das Programm einfach erweitern, um zwei Quadrate zu malen. |
 |
Das Programm wird einfach erweitert Zuerst wird das erste Quadrat gezeichnet, dann etwas verschoben das zweite Quadrat. |
Aufgabe: erweitere das bisherige Programm und überprüfe, ob das gewünschte Ergebnis erhalten wird.
Aufgabe 3: Viele Rechtecke !!!!!
Bisher waren nur sehr wenige Quadrate auf der Bühne. Wenn man sehr viele Quadrate haben möchte, dann wird das ‚Untereinanderschreiben‘ von Zeichenbefehlen sehr mühsam. Dafür sollten Programmschleifen verwendet werden.
Aufgabe: Zeichne die Rechtecke.
Das grösste Quadrat ist an Position -160, -160, die Größe ist 320.
Der Pseudocode sieht so aus:
verstecke dich
wische malspuren weg
setze xPos auf -160
setze yPos auf -160
setze xSize auf 320
setze ySize auf 320
wiederhole 32 mal
send male an alle und warte
ändere xSize um -10
ändere ySize um -10
ändere xPos um 5
ändere yPos um 5
Bei jedem Schleifendurchlauf wird die Position des Quadrats etwas verschoben und die Größe etwas kleiner.
Aufgabe 4: Zeilen und Reihen
Es ist klar, dass man „wiederhole“-Schleifen braucht.
Eine Wiederhole-Schleife für die Zeilen, und darin enthalten eine zweite Wiederhole-Schleife für die einzelnen Quadrate innerhalb der Zeile.
Aufgabe 5: Verschachtelt
Dieses Beispiel kann aus den ineinander geschachtelten Rechtecken abgeleitet werden.
Beispiellösungen